NRMSE (Normalized Root Mean Square Error)
The Normalized Root Mean Square Error (NRMSE) is a metric used in assessing the accuracy of models, particularly in the context of comparing models with different scales. It builds upon the Root Mean Square Error (RMSE), a commonly used measure of the differences between predicted values and observed values. While RMSE provides a straightforward measure of error, it can be challenging to interpret its absolute value, especially when dealing with variables of different scales.
The NRMSE addresses this issue by normalizing the RMSE, which essentially scales the RMSE value relative to the observed range of the variable. By doing so, the NRMSE offers a more standardized measure of error that can be compared across different datasets, models, or variables.
Mathematically, the NRMSE is calculated by dividing the RMSE by the range of the observed variable. This normalization process ensures that the NRMSE value is relative to the variability present in the dataset, making it more interpretable and facilitating meaningful comparisons between models or datasets with varying scales.
Interpreting the NRMSE involves understanding it as a fraction of the overall range of the variable that is typically resolved by the model. In other words, the NRMSE quantifies the proportion of the variability in the observed data that the model is able to capture. A lower NRMSE value indicates a better fit between the model predictions and the observed data, suggesting higher accuracy and reliability in the model's performance.
In practical terms, the NRMSE provides valuable insights into the effectiveness of a model in capturing the variability of the observed data, allowing researchers and practitioners to evaluate and compare different models objectively. Additionally, the normalized nature of the NRMSE makes it particularly useful when working with datasets or models of varying scales, enabling fair and meaningful comparisons across different contexts and applications.
Overall, the NRMSE serves as a valuable tool in the assessment and validation of models, offering a standardized measure of error that accounts for the inherent variability in the observed data. Its normalization properties make it an essential metric for researchers and practitioners seeking to understand and improve the accuracy of their models across diverse domains and applications.
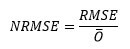
Where O represents the average of the observation values. You can find the formula for RMSE by clicking on it.
How To Cite
Please provide the data in a two-column format (observed vs. simulated). You can copy from Excel, text, or any other format, separated by space.
Normalized Root Mean Square Error: