Kendall rank correlation coefficient
The Kendall rank correlation coefficient, often denoted as τ (tau), is a non-parametric measure of correlation between two variables. Unlike Pearson correlation, Kendall's τ does not assume normality or linearity in the data, making it suitable for ordinal or ranked data. It measures the strength and direction of association between two variables by comparing the ranks of their values.
The calculation of τ involves counting the number of concordant and discordant pairs in the data. A concordant pair is when the ranks of both variables have the same direction of change (either both increasing or both decreasing), while a discordant pair is when the ranks have opposite directions of change.
The formula for Kendall's τ involves dividing the difference between the number of concordant and discordant pairs by the total number of pairs. This normalized measure ranges from -1 to 1, where τ = 1 indicates perfect positive association, τ = -1 indicates perfect negative association, and τ = 0 indicates no association.
Kendall's τ is widely used in various fields such as statistics, economics, biology, and environmental science, especially when dealing with ranked data or when the assumptions of parametric correlation measures like Pearson correlation cannot be met. Its robustness to outliers and its ability to handle tied ranks make it a valuable tool for assessing relationships between variables in diverse research contexts.
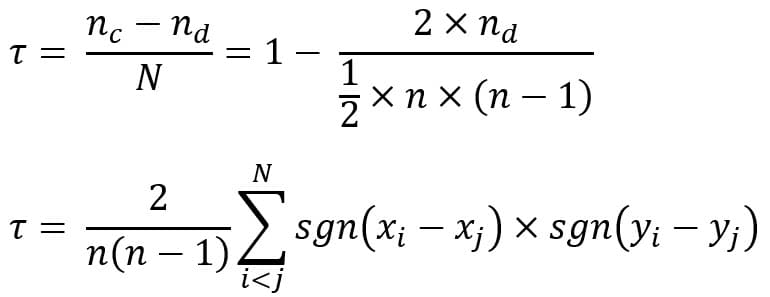
Where τ represents the Kendall rank correlation coefficient, Nc denotes the number of concordant pairs, and Nd represents the number of discordant pairs. The sgn function denotes the sign function. N stands for the total number of pairs, while n represents the number of data points.
Reference1: Link
Reference1: Link
How To Cite
Please provide the data in a two-column format (observed vs. simulated). You can copy from Excel, text, or any other format, separated by space.