Gamma Distribution Fitting
In probability theory and statistics, the gamma distribution is a versatile and widely used continuous probability distribution that belongs to a two-parameter family. This distribution finds application in various fields such as econometrics, reliability engineering, and queueing theory, among others. The gamma distribution is characterized by its shape and scale parameters, often denoted as k and θ.
The gamma distribution is particularly prevalent in econometrics and other applied fields where modeling waiting times is essential. In such contexts, the gamma distribution offers a flexible framework for capturing the distribution of waiting times, making it a valuable tool for analyzing various processes and phenomena.
One common application of the gamma distribution is in life testing, where the distribution of waiting times until an event occurs is of interest. For example, consider the waiting time until failure or death in reliability engineering or survival analysis. In these scenarios, the gamma distribution provides a suitable model for the distribution of waiting times, allowing analysts to make predictions and assess risks associated with different outcomes.
The parameterization of the gamma distribution with k and θ parameters is especially common in econometrics and reliability engineering. The parameter k represents the shape of the distribution, influencing its skewness and kurtosis, while θ controls the scale, affecting the spread or variability of the distribution. By adjusting these parameters, analysts can tailor the gamma distribution to fit observed data and make informed decisions based on the underlying statistical properties.
In summary, the gamma distribution serves as a fundamental tool in probability theory and statistics, offering a flexible framework for modeling continuous random variables, particularly in scenarios involving waiting times. Its parameterization with shape and scale parameters facilitates its application in various fields, allowing analysts to capture the distributional characteristics of data and make reliable inferences about the processes under study.
The probability density function using the shape-scale parametrization is:
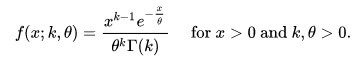
Where:
-
θ is the scale parameter
-
K is the shape parameter
How To Cite
We used Accord.Statistics for this calculator