Poisson Distribution Fitting
The Poisson distribution serves as a fundamental concept in probability theory, providing a framework for modeling the occurrence of rare events over a fixed period of time. It represents a discrete probability distribution that quantifies the likelihood of a specific number of events occurring within a defined time interval, given a known average rate of occurrence. Crucially, the events must manifest independently of one another and exhibit a constant average rate throughout the observation period.
Imagine scenarios where rare events, such as customer arrivals at a service center, radioactive decay events in a sample, or traffic accidents at an intersection, are being studied. The Poisson distribution offers a means to predict the probability of observing a certain number of such events within a specified time frame, given the average rate at which these events typically occur.
Key characteristics of the Poisson distribution include its assumption of independence between events, meaning that the occurrence of one event does not influence the likelihood of another event happening. Additionally, the distribution assumes a constant average rate of event occurrence over the entire observation period.
Mathematically, the probability mass function of the Poisson distribution is defined by a single parameter, often denoted as λ (lambda), representing the average rate of event occurrence per unit time. This parameter governs the shape and spread of the distribution, with higher values of λ corresponding to a greater likelihood of observing a larger number of events within the specified time interval.
Applications of the Poisson distribution abound across various fields, including telecommunications, biology, finance, and epidemiology. It finds utility in predicting the number of calls arriving at a call center within a given hour, estimating the number of mutations occurring in a DNA sequence, modeling the frequency of rare financial events, and assessing the incidence of disease outbreaks.
In summary, the Poisson distribution provides a powerful tool for modeling the occurrence of rare events over fixed time intervals. Its simplicity and flexibility make it invaluable for a wide range of applications, allowing researchers and practitioners to make informed decisions and predictions based on probabilistic assessments of event frequency.
References:
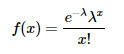
Where:
- λ is the average number of events per interval
- e is the number 2.71828... the base of the natural logarithms
- x takes values 0, 1, 2,...
- x! = x × (x - 1) × (x - 2) × ... × 2 × 1 is the factorial of x.
How To Cite
We used Accord.Statistics for this calculator