Gumbel Distribution Fitting
In probability theory and statistics, the Gumbel distribution is used to model
the distribution of the maximum (or the minimum) of a number of samples of various
distributions. Such a distribution might be used to represent the distribution of
the maximum level of a river in a particular year if there was a list of maximum
values for the past ten years. It is useful in predicting the chance that an extreme
earthquake, flood or other natural disaster will occur.
The potential applicability of the Gumbel distribution to represent the distribution
of maxima relates to extreme value theory which indicates that it is likely to be useful
if the distribution of the underlying sample data is of the normal or exponential type.
The Gumbel distribution is a particular case of the generalized extreme value
distribution (also known as the Fisher-Tippett distribution). It is also known
as the log-Weibull distribution and the double exponential distribution (a term
that is alternatively sometimes used to refer to the Laplace distribution). It
is related to the Gompertz distribution: when its density is
first reflected about the origin and then restricted to the positive half line,
a Gompertz function is obtained.
In the latent variable formulation of the multinomial logit model - common in
discrete choice theory - the errors of the latent variables follow a Gumbel
distribution. This is useful because the difference of two Gumbel-distributed
random variables has a logistic distribution.
The Gumbel distribution is named after Emil Julius Gumbel (1891-1966), based on
his original papers describing the distribution.
References:
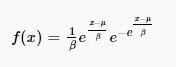
Where:
We used Accord.Statistics for this calculator
