Normal Distribution Fitting
The normal distribution stands as the cornerstone of statistical distributions, renowned for its ubiquity and versatility. Widely applied across various disciplines, it serves as the foundation for numerous other distributions derived from its properties. Normal distributions play a pivotal role in statistics, offering a reliable framework to model real-valued random variables whose distributions remain unspecified.
One of the key strengths of the normal distribution lies in its ability to accurately describe the behavior of a wide array of phenomena observed in both natural and social sciences. From physical measurements to socioeconomic indicators, the normal distribution provides a robust statistical model for understanding and analyzing complex datasets. Its symmetrical bell-shaped curve, characterized by a central peak and symmetric tails, makes it particularly well-suited for describing phenomena where values cluster around a central tendency while exhibiting variability.
In addition to its descriptive power, the normal distribution holds significance in inferential statistics, enabling researchers to make probabilistic statements about populations based on sample data. The central limit theorem, a fundamental concept in statistics, underscores the normal distribution's importance by stating that the sampling distribution of the sample mean tends to follow a normal distribution, regardless of the underlying population distribution.
Moreover, the normal distribution finds application in various statistical techniques, such as hypothesis testing, confidence interval estimation, and regression analysis. Its mathematical properties, including well-defined moments and easily calculable probabilities, simplify statistical calculations and facilitate rigorous statistical inference.
Beyond its statistical applications, the normal distribution has profound implications in practical decision-making processes. From quality control in manufacturing to risk assessment in finance, the normal distribution serves as a fundamental tool for making informed decisions based on data-driven insights.
In summary, the normal distribution's prominence stems from its versatility, mathematical elegance, and wide-ranging applicability across diverse domains. As the quintessential statistical distribution, it continues to play a central role in advancing scientific knowledge, informing policy decisions, and driving innovation in countless fields.
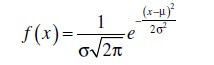
Where:
-
μ is the mean of samples in distribution or continuous location parameter
-
σ is the standard deviation or continuous scale parameter (> 0)
How To Cite
We used Accord.Statistics for this calculator