Uniform Continuous Distribution Fitting
The uniform continuous distribution, also known as the rectangular distribution, comprises a family of symmetric probability distributions wherein all intervals of equal length on the distribution's support possess equal probability. This distribution is characterized by two parameters, denoted as a and b, representing its minimum and maximum values, respectively. Typically abbreviated as U(a,b), it encapsulates the concept of maximum entropy probability distribution for a random variate X, under the sole constraint that it falls within the distribution's defined support.
The uniform continuous distribution exhibits a flat, constant probability density function across its entire support interval [a, b]. This uniformity implies that every value within the support interval has an equal likelihood of being observed. The distribution's simplicity and symmetry render it a foundational model in probability theory and statistics, with diverse applications across various fields.
One notable property of the uniform continuous distribution is its maximum entropy characteristic. Entropy, in this context, refers to the measure of uncertainty or randomness associated with a probability distribution. The uniform distribution, with its uniform probability density function, maximizes entropy among all distributions constrained only by the bounds of its support interval [a, b]. This property underscores the uniform distribution's significance as a default choice when no prior information or constraints are available regarding the underlying random variable's behavior.
Applications of the uniform continuous distribution span numerous domains, including engineering, finance, physics, and computer science. In engineering, it finds utility in modeling scenarios such as uniform flow rates or temperatures within specified bounds. In finance, it may be employed to represent random fluctuations in asset prices over a defined range. In physics, the uniform distribution may describe the spatial distribution of particles within a confined region. Furthermore, in computer science, it serves as a foundational concept in generating random numbers uniformly across a given range.
In summary, the uniform continuous distribution embodies the principle of equal probability across a defined interval, making it a versatile and fundamental tool in probability theory and applied statistics. Its maximum entropy property and widespread applicability underscore its importance in various fields, where it facilitates the modeling and analysis of diverse phenomena characterized by uniformity and randomness.
References:
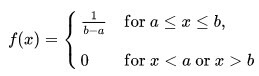
Where:
-
a is lower bound
-
b is upper bound
How To Cite
We used Accord.Statistics for this calculator