Bernoulli Distribution Fitting
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,[1] is the discrete probability distribution of a random variable which takes the value 1 with probability {\displaystyle p} p and the value 0 with probability {\displaystyle q=1-p,} {\displaystyle q=1-p,} that is, the probability distribution of any single experiment that asks a yes?no question; the question results in a boolean-valued outcome, a single bit of information whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails" (or vice versa), respectively, and p would be the probability of the coin landing on heads or tails, respectively. In particular, unfair coins would have {\displaystyle p\neq 1/2.} {\displaystyle p\neq 1/2.}
The binomial distribution is the discrete probability distribution of the number of
successes in a sequence of >n independent yes/no experiments, each of which
yields success with probability p. Such a success/failure experiment is also
called a Bernoulli experiment or Bernoulli trial; when n = 1, the binomial
distribution is a Bernoulli distribution.
References:
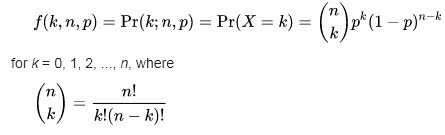
Where:
p is the success probability for each trial
q is the failure probability for each trial
f(k,n,p) is probability of k successes in n trials when the success probability is p
We used Accord.Statistics for this calculator
