Gamma Distribution Fitting
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The parameterization with k and θ appears to be more common in econometrics and certain other applied fields, where for example the gamma distribution is frequently used to model waiting times. For instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution.
The probability density function using the shape-scale parametrization is:
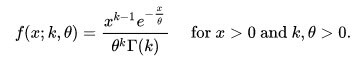
Where:
θ is the scale parameter
K is the shape parameter
We used Accord.Statistics for this calculator
