Gumbel Distribution Fitting
The Gumbel distribution, a fundamental concept in probability theory and statistics, serves to model the distribution of maximum or minimum values derived from multiple samples across various distributions. It finds practical application in scenarios like predicting extreme events such as earthquakes, floods, or other natural disasters.
One of its key applications lies in representing the distribution of maximum river levels over a specified period, such as the highest river level recorded annually over the past decade. This distribution offers insights into the likelihood of extreme events occurring, aiding risk assessment and disaster management efforts.
The suitability of the Gumbel distribution hinges on its relation to extreme value theory, particularly when the underlying sample data follows a normal or exponential distribution pattern. As a specific case of the generalized extreme value distribution, the Gumbel distribution shares its origins with the Fisher-Tippett distribution.
Interestingly, the Gumbel distribution holds significance beyond its direct applications. In discrete choice theory, it appears in the latent variable formulation of the multinomial logit model. Here, errors in latent variables conforming to a Gumbel distribution facilitate modeling choice behavior, as the difference between two Gumbel-distributed random variables yields a logistic distribution.
Emil Julius Gumbel, the namesake of this distribution, contributed significantly to its development through original papers elucidating its properties and applications. His work has cemented the Gumbel distribution's place as a cornerstone in statistical theory and practical modeling endeavors.
References:
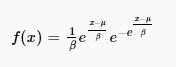
Where:
-
μ is the location parameter
-
β is the scale parameter
How To Cite
We used Accord.Statistics for this calculator