Normal Distribution Fitting

The normal distribution is the most famous of all distributions. It is applied directly to many samples, and several valuable distributions are derived from it. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known.

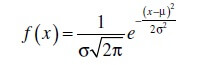
Where:

• μ is the mean of samples in distribution or continuous location parameter

• σ is the standard deviation or continuous scale parameter (‹ 0)

We used Accord.Statistics for this calculator

Paste a column data here. In format of excel, text, etc. Each sample in one line.

Calculate the probability of the fitted distribution on: Normal Distribution Calculator

Normal Distribution: